11.1 Light
Visible light ranges from red through yellow and green to blue and violet. Newton was the first to discover that white light is a mixture of all the colors. White light can be split into its component colors by diffraction through a prism, which ‘bends’ each color by a different amount. A diffractiongrating is often used in astronomy because tiny or dim light sources suffer less energy loss in reflecting from a hard, ruled surface than is lost traveling through a glass prism.
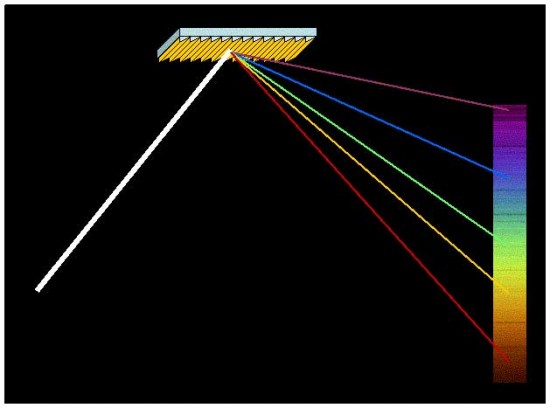
White light can be separated into its component colors by reflecting from a finely-grooved flat metal grating, courtesy NASA, Jet Propulsion Laboratory
Eventually, Maxwell, who defined the Electromagnetic Field equations, proved that light was in fact made up of electromagnetic (EM) waves. Each color of visible light has a characteristic frequency and wavelength. As with all waves, the product of frequency and wavelength give the velocity of the wave. Obviously, light travels at the velocity of light, but Maxwell was able use his equations to shown that all electromagnetic waves travel with the velocity of light, and so light must also be an electromagnetic wave.
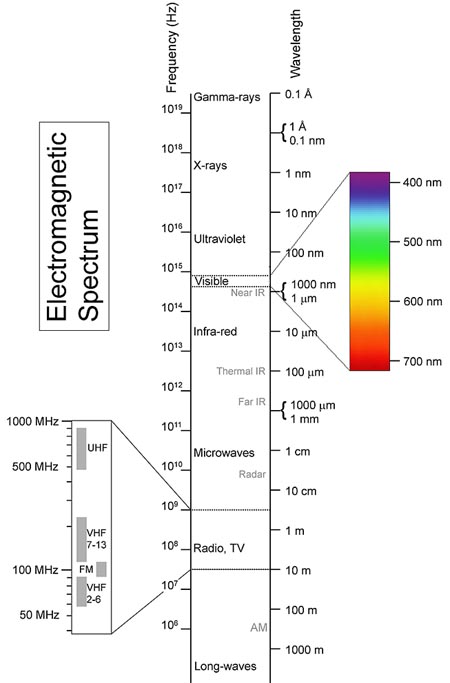
Visible light represents only a small part of all the possible frequencies or wavelengths. The whole range is known as the electromagnetic spectrum.
11.2 The Spectrum
Although the spectrum is continuous, each region of the spectrum has been named after a typical type of wave for that part of the spectrum.
Starting with the lowest-frequency, longest-wavelength waves, the spectrum runs from radio waves through microwaves (as in ovens), terahertz radiation (a recent development in military communications), infrared (as in heaters), the visible spectrum (Red, Orange, Yellow, Green, Blue, Indigo, Violet), ultraviolet (tanning and forensic lamps, materials analysis), X-rays (internal medical images), and up to Gamma rays (cancer treatments).
The spectrum is shown in the following diagram. Note that the visible spectrum is only a small part of the whole spectrum. When the Gravity Model was formulated, scientists could only see visible light from the heavens.
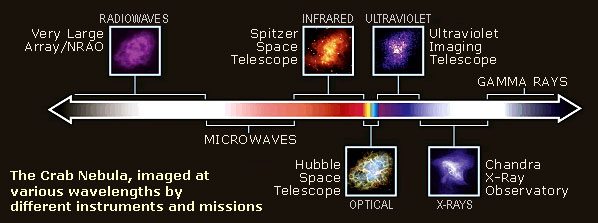
Diagram of the electromagnetic spectrum, with images of the Crab nebula showing how it would “look” if we could see beyond the limits of our eyes’ light sensitivity range, courtesy NASA
In the 20th century, and especially since the start of the Space Age in the 1950s, instruments have been developed which allow scientists to detect virtually all wavelengths. The amount of information available has increased exponentially. Observations are often surprising because what is seen in the visible is seldom anything like what is found at other wavelengths.

Jupiter as seen in optical wavelengths (grayscale), with its auroras radiating in invisible X-ray radiation (mapped to visual violet as “false color” to appear visible to us). Image credit: NASA / Chandra X-ray Telescope
11.3 Radiation
Radiation is the process whereby energy is emitted by one body, transmitted through a medium or through space, and eventually absorbed by another body. The emitting and absorbing bodies can be as small as individual atoms or even subatomic particles like electrons.
Electromagnetic waves are the means whereby the energy is transmitted. In other words, all radiation is electromagnetic.
This means that the mode of transmission of radiation involves oscillating electric and magnetic fields which carry the energy similar to the way that vibrations on a string carry energy along the string. Since the speed of transmission of vibrational energy is constant for a given medium, and that value is equal to the frequency of the vibrating wave times the wavelength (frequency times wavelength = velocity), if you know the frequency one can solve for the wavelength at that frequency, and vice versa.
The spectrum represents the range of possible frequencies or wavelengths of the radiation. As the frequency increases, the amount of energy carried by the wave also increases in proportion to the frequency. Ionizing radiation is radiation which carries sufficient energy to ionize atoms. In general terms, frequencies from radio to the visible do not carry enough energy for this, while ultraviolet, X-ray and Gamma ray radiation can ionize. As noted previously, ionization energy varies with different elements and molecules.
Radiation is emitted whenever a charged particle undergoes acceleration. Remembering that a change of direction is also an acceleration because the direction of the velocity is changing, then every charged particle that experiences a change of direction will emit radiation.
Current theories explain this emission in terms of the emission of a photon, or packet of energy. A photon has no mass but carries the radiated energy in the form of electromagnetic waves. A photon behaves both like a wave and like a particle. Which mode is more significant will depend on the circumstances.
To summarize:
- Radiation is emitted by all charged particles undergoing acceleration.
- All radiation involves electromagnetic waves.
- Radiation transmits energy.
- The spectrum represents the range of possible frequencies or wavelengths of the radiation.
11.4 Thermal radiation
Thermal radiation is radiation emitted from a surface of a body or region of particles due to the temperature of the body or region.
Temperature is a measure of the thermal energy contained in a body. The thermal energy causes the charged particles inside the atoms of the body to vibrate in a random fashion. They will therefore emit radiation over a range of frequencies. Similarly, a region of plasma can have a temperature.
A proportion of this radiation is emitted from the surface of the body or region as heat (infrared radiation). Actually, all matter with any internal thermal motion radiates EM energy: the colder it is, the longer the wavelength it radiates. Cold interstellar dust will radiate terahertz, or sub-millimeter wavelength radiation, starting at a temperature of only about 10 Kelvin.

Cold Saturn’s deep nighttime hemisphere imaged in infrared radiation by Cassini’s thermal/optical mapping spectrometer in 2006. Image courtesy, NASA / JPL / Cassini Imaging Team
Because of the random nature of the vibrations over a large number of particles, the emitted radiation will have a range of frequencies, or wavelengths. Statistical analysis shows that in an ideal situation the energy emitted at any one wavelength is a function of that wavelength. This is known as Planck’s Law and is shown graphically below for a range of temperatures. The radiation emitted in this ideal situation is known as Blackbody radiation, which simply means that it has the distribution pattern that would be expected from a perfect emitter in thermal equilibrium. (Diagram source: Wikipedia ‘blackbody‘ article)
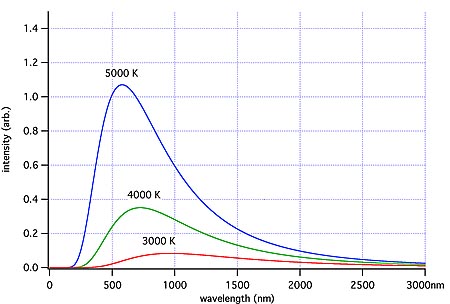
Ideal blackbody radiation for 3 temperatures, showing that the peak wavelength emitted shifts to higher frequencies (shorter wavelengths) with increasing temperature. Image credit: Wiki Commons
The graphs show that for any one temperature there is one wavelength at which the greatest amount of energy is emitted. As the temperature increases, the wavelength of the peak energy decreases. This is defined by another law known as Wien’s Law. Note that the red line has a lower temperature and lower area under its curve than the hotter blue line.
The area under any one temperature curve gives the total amount of energy emitted at that temperature, per unit area. The total energy emitted per unit area depends only on the temperature. This is known as the Stefan-Boltzmann Law.
If the pattern of emitted radiation from any source is distributed in the form given by Planck’s Law, then the emission is assumed to be due to random thermal movements of particles in the source. We then say that the radiation is thermal radiation. All this means is that the radiation has a distribution of wavelengths or frequencies which come from the random thermal vibrations of particles. The radiation itself is electromagnetic radiation like any other radiation.
If we find that radiation is thermal, then we can determine the temperature of the source by comparing the emitted radiation curve to the ideal ‘Black Body’ curves. This means we can determine the temperature of distant objects if the radiation they emit is thermal radiation. Stars have been found to have a spectrum which approximates a blackbody distribution, so the color temperature of stars can be inferred from their spectra.
Non-thermal radiation is simply radiation which is not emitted in a thermal pattern. It must therefore be generated by other methods than random temperature-induced motions of the particles in a system in thermal equilibrium.
That is not to say that temperature cannot play a part in causing these other patterns of radiation; it is simply that the system or body that is emitting the radiation is not in thermal equilibrium. In other words, energy is being exchanged with the system so that its temperature is changing with time. This will alter the ideal Black Body pattern of radiation and mean that it is not possible to assign a temperature to the body.
Alternatively, the radiation may be emitted by individual particles undergoing acceleration caused by means other than random collisions with other particles.
11.5 Optical Radiation in the Cosmos
Radiation in the cosmos is common in the visible and radio wavelengths. In the optical region, the majority of radiation is generated by electrons jumping to new orbits within an atom (bound-bound transitions), free electrons recombining with ions to form neutral atoms (free-bound transitions) and electrons being decelerated by interaction with other material (free-free radiation).
The bound-bound transitions are a source of both emission lines and absorption lines in the spectrum. Each chemical element has a range of energies associated with the range of possible electron orbits around the nucleus for that element. As an electron jumps from one orbit to another, energy in the form of radiation is either absorbed or given off. The energy represents the difference in the orbital energies and so is precisely defined for each possible jump between levels.
Because the energy of a photon is proportional to its frequency, these energy differences will result in radiation with a defined set of frequencies for each element. If the radiation energy emitted from an element is plotted for each frequency in the spectrum, then there will be sharp peaks in the graph at these frequencies. These are known as emission lines in the spectrum.
On the other hand, if light with a broad range of frequencies passes through a medium containing certain elements or molecules, those elements are found to absorb energy at their characteristic frequencies. The resulting spectrum will be missing those frequencies, and dark lines will appear. These are known as absorption lines.
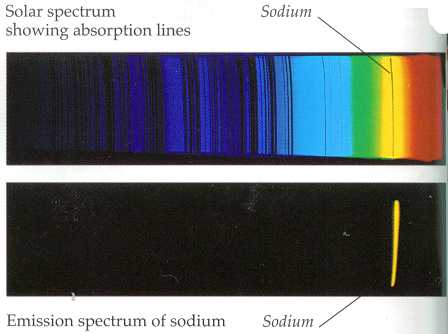
Lower, the primary yellow-light sodium emission line, from heated sodium atoms. Above is an absorption spectrum where light from a blackbody-like source (such as a star) has passed through a volume of space containing sodium on its way to the observer or imaging instrument. The black line is where the sodium atoms have absorbed light preferentially at that frequency, leaving a dark line at that “color”. Image courtesy of ThinkQuest (www.thinkquest.org), funded by the Oracle Education Foundation
Here is an introduction to blackbody radiation and absorption lines and continuum radiation. And here is moreto explore in the broader context of spectroscopy.
As an example, if an element is heated in a star’s interior, then it will give off its characteristic radiation which we can detect as bright emission lines on Earth. On the other hand, if broadband light has passed through an absorbing medium between the observer and the light source, then we can determine the elements in that medium by looking for the dark absorption lines.
Free-bound transitions occur when electrons are captured by ions and result in release of energy as recombination occurs. The amount of energy released is dependent on the element formed and the orbit that the electron occupies. As in the bound-bound transition, certain frequencies may dominate.
Free-free radiation occurs when electrons undergo a non-capture collision with an ion or a charged dust particle in the plasma. The electron’s trajectory will be changed as it passes near the other particle, and so it will give off radiation, some of which may be in the visible spectrum.
11.6 Radio Radiation in the Cosmos
Radio wavelengths are important because many radio waves can penetrate the Earth’s ionosphere and so can be detected by ground-based radio telescopes.

Radio telescope array in New South Wales, Australia. Image credit, University of Waikato and Commonwealth Scientific and Industrial Research Organisation (CSIRO)
Some radio radiation in the cosmos is a result of the collective behavior of large numbers of electrons in a plasma. If the plasma is sufficiently dense, then the electrons can oscillate collectively with a frequency known as the plasma frequency, which depends only on the density of the electrons in the region. These oscillations generate radiation in the usual way.
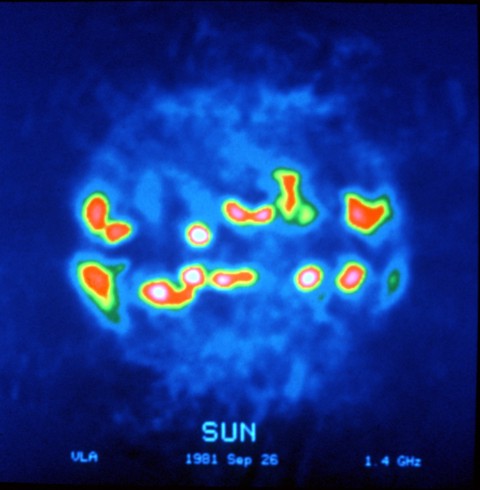
The Sun, as seen (in false color) at a radio wave frequency of 1.4 GHz, with strong emissions at the active regions in the solar equatorial belt. Image courtesy of the National Radio Astronomy Observatory (NRAO/AUI)
This type of radiation often occurs when a beam of electrons, for example, as might be generated by acceleration through a double layer, passes through a region of neutralizing plasma.
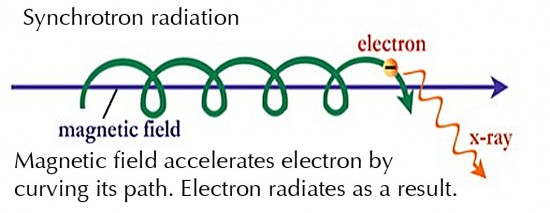
There are other radio frequency radiation generating mechanisms where a magnetic field is present. These include cyclotron radiation (where electrons have non-relativistic velocities), Magneto-Bremsstrahlung radiation (where electrons have mildly relativistic velocities), and synchrotron radiation (where electrons have relativistic velocities).
Synchrotron radiation is produced by electrons spiraling along the direction of a magnetic field, such as occurs in Birkeland Currents (image in 11.3 above). The centripetal acceleration causes the radiation. Again, the radiation can occur at all frequencies across the spectrum.
In astrophysics, non-thermal radio emission is, in most cases, synchrotron radiation. This is true for galactic radio emissions, supernovae envelopes, double radio galaxies, and quasars. Additionally, the Sun and Jupiter both produce sporadic synchrotron emissions.
Synchrotron emission can also generate optical frequencies, such as are seen in the Crab Nebula and the M87 ‘jet’. The Crab Nebula (short YouTube video) also emits quantities of X ray synchrotron radiation.
The analysis of a synchrotron spectrum can give information on the source of the relativistic electrons, which may have a bearing on the origin of cosmic rays, X rays, and Gamma rays in space. Synchrotron radiation is also evidence for the existence of extensive magnetic fields in space and for the conversion, storing, and releasing of large amounts of energy in cosmic plasmas, including galactic jets. More details on synchrotron radiation herefor the interested explorer.
Z-pinches can also generate synchrotron radiation as a result of the v × B force.
Radio astronomy can therefore extend the range of information available to us well beyond that derivable from visual telescopes alone. Detection of higher energy spectra such as X-rays can take this knowledge a stage further.

Active galaxy Centaurus A (NGC 5128) , composite image in sub-millimeter (radio plumes; orange), visible (white) and X-ray radiation (blue). Galaxy’s diameter is approximately 200,000 light years; estimated distance 10 million light years. Credit: X-ray: NASA/CXC/Cfa/R. Kraft et al.: sub-millimeter: MPIfR/ESO/APEX/A.Weiss et al. Optical: ESO/WFI
A short NASA video on this galaxy is here, although the EU does not speculate about black holes’ causing galactic jets and their resultant radiation.
In all cases we find that plasmas and electric currents within them are excellent emitters of radiation because, as we have seen, electricity in plasma is extremely good at accelerating charged particles, via the electric fields across double layers, which particles then emit the radiation. Interesting research arXiv article posted here.

Arcades of solar plasma filaments in the lower corona of the Sun are revealed in far ultraviolet light by TRACE instruments, courtesy The TRACE Picturebook, NASA
This efficient production of radiation by electrical mechanisms seems to be a much more likely source of most of the radiation detected in space than are the huge amounts of Dark Matter and super-dense matter necessary to explain particle acceleration using only gravity.
Of course, ‘magnetic reconnection’, the alleged breaking and reconnection of magnetic field lines, is also often invoked to explain this type of evidence in the Gravity Model. As we have seen, this is simply impossible because magnetic field lines don’t have a physical existence any more than lines of longitude do.
End of Chapter 11
Appendix I – Vector Algebra
Vector algebra is formulated to handle vectors; i.e., quantities with both magnitude and direction. Normal algebra, geometry and trigonometry are efficient at dealing with scalar quantities, that is, those with only magnitude, but are inefficient at handling vectors. Vector algebra is an efficient way of solving 2D and 3D problems involving vectors without the need for cumbersome geometry.
The electro-magnetic (e/m) field is a vector field of forces acting on charged objects. As forces are vector quantities (forces acting in an associated direction), the e/m field equations involve vectors.
Vector algebra can be formulated for Cartesian, cylindrical and spherical coordinates. Appropriate choice of coordinate system for cylindrically or spherically symmetric problems avoids needless complexity arising from the use of an inappropriate coordinate system and will also clearly show the symmetry of the solution.
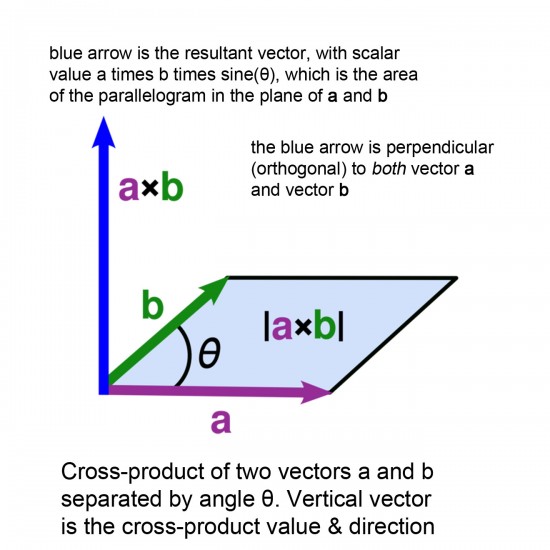
Two important results of vector algebra involve multiplication of vectors. Vectors will be indicated by bold text.
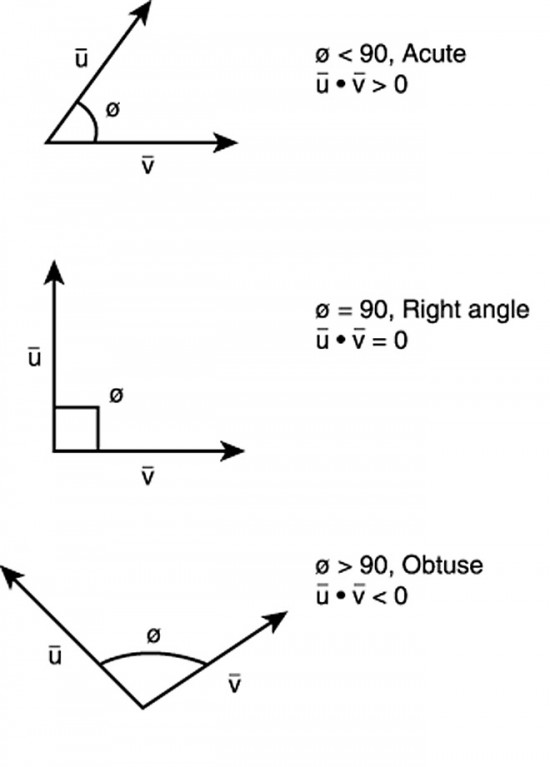
The dot product (or “scalar” product) A・B (read as “A dot B”) is defined as ||AB|| cos(θ) where A and B are the magnitudes (numeric values) of the vectors A and B respectively and θ is the angle between them. Note that the dot product is a scalar quantity ( a simple numeric value (magnitude) without an associated direction), and geometrically is in a single plane (i.e., 2D). If the angle between two vectors > 90° then the scalar is negative (<0). If two vectors are perpendicular to one another, their dot product is zero.
The cross product A×B (read as “A cross B”) is defined as AB sin(θ)an, where an is the unit vector normal to the plane of A and B. Note that the cross product of two vectors is also a vector and its direction is orthogonal (perpendicular) to both A and B; i.e., the resultant vector involves a third dimension compared to the 2D plane containing the first two vectors.
Vector algebra defines another important operator, Del, or Δ. Del is analogous to the differential operator D in calculus where D represents the operation d/dx. Two further results using Del are important in analyzing e/m fields.
Δ・A or Div A is the divergence of the vector field A. The divergence is a scalar and is similar to the derivative of a function. If the divergence of a region of a vector field is non-zero then that region is said to contain sources (Div A>0) or sinks (Div A<0) of the field. For example, an arbitrary closed surface around an isolated positive charge in a static electric field contains the source of the electric flux, that is the positive point charge; therefore the divergence of the electric flux density vector field over that surface will be positive, and equal to the enclosed charge. This is Gauss’ Law. (see Appendix II, e/m field equations)
Note that Div A involves a dot product and is therefore dependent on angles. The angle is usually that between the vector and the normal to the surface being analyzed.
Δ×A or Curl A is the curl of the vector field A. The curl of a vector field is another vector field which describes the rotation of the first vector field; the magnitude of Δ×A is the magnitude of the rotation, and the direction of Δ×Ais the axis of that rotation as determined by the right-hand rule. If one imagines any 3D vector field to represent fluid flow velocities, then the curl of the field at a point would be indicated by the way a small sphere or a paddlewheel placed at that point would be rotated by the flow. In a 2D flow it is easy to see that the direction of the axis of rotation of a circle (the 2d analogue of a sphere) in the flow will be in the third dimension, as is given by the use of the cross product in calculating the curl.
Additionally, the Del operator can be applied to a scalar field V. ΔV or Grad V is a vector field defining the gradient of the scalar function V. ΔV lies in the direction of the maximum increase of the function V. If applied to a potential function, then Grad V is a vector field that is everywhere normal to the equipotential surfaces.
Two useful properties of the Curl operator are:
(1) the divergence of the curl of any vector field is the zero scalar; i.e., Δ・(Δ×A) = 0
(2) the curl of a gradient of any vector field is the zero vector; i.e. Δ×(Δf) = 0 for any scalar function f dependent on position, as in f(x,y,z)
Example: To visualize (2), think of a scalar field such as an area of hilly land, where contours of constant elevation above sea level are “drawn” along the ground. Elevation “h” at any given point (x,y,z) would then vary with position, so its function is h(x,y,z). The gradient del(h) would be a vector that points, starting at the point (x,y,z), perpendicular to the contour line through (x,y,z) and straight “down the hill”. Imagine the way water flows downhill, or which way a marble would roll, and that’s the direction the gradient vectors point, always perpendicular to the equal-elevation contour at any point. Because these vectors are straight, they have no curl, or bend. That’s why, mathematically, ‘del × (del h) = 0′.
In practice, this means that an electric field in which the lines of flux are straight (e.g., between the layers of a plasma double layer or a capacitor, ignoring edge effects where the lines are not straight), a charged particle will be accelerated from rest in a straight line: the electric field has no curl.
Vector algebra becomes even more important in analyzing particle interactions when several forces may be present, as when a charged particle enters both an electric field and an associated magnetic field simultaneously, at an oblique angle so that its motion vector can have one component normal to the field lines and another (“drift”) parallel to them. The Mathematica©-based images in Chapter 4, ¶4.3, are indicative of some of the complexities of such interactions using only 1 particle. Plasma are double digit orders of number of particles higher than this simplest case, and the feedback mechanisms and complex particle motions that develop cause the plasma to create and maintain charge separation, to separate bodies with one electrical field potential from a volume of differente potential, to initiate current flows, to accelerate particles to relativistic velocities and radiate strongly, to pinch and roll up current sheets into filamentary conducting plasma structures like lightning, coronal loops and galactic jets.

TRACE imagery of current loop arcades and prominences above an active region on the Sun
Appendix II: The Electro-magnetic Field Equations
Introduction
Maxwell’s Equations and the Lorentz Force Law together comprise the e/m field equations; i.e., those equations determining the interactions of charged particles in the vicinity of electric and magnetic fields and the resultant effect of those interactions on the values of the e/m field.
For ease of explanation, the following will refer to “fields” as though they possess some independent physical reality. They do not. The use of fields is as an aid in understanding how forces exerted by and upon real particles, and how the positions (coordinates) of those particles may exist at a given time, or may vary over an interval of time. Field lines are also convenient notational devices to aid in understanding what physically is going on, and are not “real”. An oft-used example is the set of lines or contours of equal elevation relative to some fixed reference value, often found on topographic maps of land areas, and varying pressure distributions on weather charts. Such lines do not exist as real physical entities; they can be used for calculation and visualization of simple or complex phenomena, but they do not effect changes or position or exert force or anything else, themselves. Imagining that they are real is called reification; it can be a convenient aid to better understanding, but it is incorrect to say that field lines of any type are real or “do” anything.
The implications of Maxwell’s Equations and the underlying research are:
- A static electric field can exist in the absence of a magnetic field; e.g., a capacitor with a static charge Q has an electric field without a magnetic field.
- A constant magnetic field can exist without an electric field; e.g., a conductor with constant current I has a magnetic field without an electric field.
- Where electric fields are time-variable, a non-zero magnetic field must exist.
- Where magnetic fields are time-variable, a non-zero electric field must exist.
- Magnetic fields can be generated in two ways other than by permanent magnets: by an electric current, or by a changing electric field.
- Magnetic monopoles cannot exist; all lines of magnetic flux are closed loops.
The Lorentz Force Law
The Lorentz Force Law expresses the total force on a charged particle exposed to both electric and magnetic fields. The resultant force dictates the motion of the charged particle by Newtonian mechanics.
F = Q(E + U×B) (remember, vectors are given in bold text)
where F is the Lorentz force on the particle; Q is the charge on the particle; E is the electric field intensity (and direction); and B is the magnetic flux density and direction.
Note that the force due to the electric field is constant and in the direction of E, so will cause constant acceleration in the direction of E. However, the force due to the combination of the particle’s velocity and the magnetic field is orthogonal to the plane of U and B due to the cross product of the two vectors in vector algebra (Appendix I). The magnetic field will therefore cause the particle to move in a circle (to gyrate) in a plane perpendicular to the magnetic field.
If B and E are parallel (as in a field-aligned current situation) then a charged particle approaching radially toward the direction of the fields will be constrained to move in a helical path aligned with the direction of the fields; that is to say, the particle will spiral around the magnetic field lines as a result of the Lorentz force, accelerating in the direction of the E field.
Further Discussion of Maxwell’s Equations
The Maxwell Equations are the result of combining the experimental results of various electric pioneers into a consistent mathematical formulation, whose names the individual equations still retain. They are expressed in terms of vector algebra and may appear, with equal validity, in either the point (differential) form or the integral form.
The Maxwell Equations can be expressed as a General Set, applicable to all situations; and as a “Free Space” set, a special case applicable only where there are no charges and no conduction currents. The General Set is the one which applies to plasma:
where
- E is the electric field intensity vector in newtons/coulomb (N/C) or volts/meter (V/m)
- D is the electric flux density in C/m2; D = εE for an isotropic medium of permittivity ε
- H is the magnetic field strength and direction in amperes/meter (A/m)
- B is the magnetic flux density in A/N・m, or tesla (T); B = μH for an isotropic medium of permeability μ
- Jc is the conduction current density in A/m2; Jc = σE for a medium of conductivity σ
- ρ is the charge density, C/m3
Gauss’ Law states that “the total electric flux (in coulombs/m2) out of a closed surface is equal to the net charge enclosed within the surface”.
By definition, electric flux ψ originates on a positive charge and terminates on a negative charge. In the absence of a negative charge flux “terminates at infinity”. If more flux flows out of a region than flows into it, then the region must contain a source of flux; i.e., a net positive charge.
Gauss’ Law equates the total (net) flux flowing out through the closed surface of a 3D region (i.e., a surface which fully encases the region) to the net positive charge within the volume enclosed by the surface. A net flow into a closed surface indicates a net negative charge within it.
Note that it does not matter what size the enclosing surface is – the total flux will be the same if the enclosed charge is the same. A given quantity of flux emanates from a unit of charge and will terminate at infinity in the absence of a negative charge. In the case of an isolated single positive charge, any sphere, for example, drawn around the charge will receive the same total amount of flux. The flux density D will reduce in proportion (decrease per unit area) as the area of the sphere increases.
Gauss’ Law for Magnetism states that “the total magnetic flux out of a closed surface is zero”.
Unlike electric flux which originates and terminates on charges, the lines of magnetic flux are closed curves with no starting point or termination point. This is a consequence of the definition of magnetic field strength, H, as resulting from a current (see Ampere’s Law, below), and the definition of the force field associated with H as the magnetic flux density B = μH in teslas (T) or newtons per amp meter (N/Am).
Therefore all magnetic flux lines entering a region via a closed surface must leave the region elsewhere on the same surface. A region cannot have any sources or sinks. This is equivalent to stating that magnetic monopoles do not exist.
Ampere’s Law with Maxwell’s Correction
Ampere’s Law is based on the Biot-Savart Law
dH = (I dl×ar) / 4πR2
which states that “a differential (i.e., tiny segment of) magnetic field strength dH at any point results from a differential current element I dl of a closed current path of current I). The magnetic field strength varies inversely with the square of the distance R from the current element and has a direction given by the cross-product of I dl and the unit vector ar of the line joining the current element to the point in question. The magnetic field strength is also independent of the medium in which it is measured.
As current elements have no independent existence, all elements making up the complete current path, i.e., a closed path, must be summed to find the total value of the magnetic field strength at any point. Thus:
H = ∫ (I dl×ar) / 4πR2
where the integral is a closed line integral which may close at infinity.
Thence, for example, an infinitely long straight filamentary current I (closing at infinity) will produce a concentric cylindrical magnetic field circling the current in accordance with the right-hand rule, with strength decreasing with the radial distance r from the wire, or:
H = (I/2πr) ar
(note the vector notation in cylindrical coordinates; the direction of H is everywhere tangential to the circle of radius r)
Ampere’s Law effectively inverts the Biot-Savart Law and states that “the line integral of the tangential component of the magnetic field strength around a closed path is equal to the current enclosed by the path”, or
∫H・dl = Ienc where the integral is a closed line integral
Alternatively, by definition of curl, Curl H or Δ×H = J, the current density.
This effectively means that a magnetic field will be generated by an electric current.
However, this only applies to time-invariant currents and static magnetic fields. As Jc = σE, this implies that the electric field is constant as well.
To overcome these restraints so as to allow for time-varying charge density and to allow for the correct interpretation of the propagation of e/m waves, Maxwell introduced a second term based on the Displacement Current, JD, where
JD = δD/δt
arising from the rate of change of the electric field E.
Maxwell’s correction, as included in the revised Law, dictates that a magnetic field will also arise due to a changing electric field.
Faraday’s Law states that “if the magnetic flux Φ, linking (i.e., looping through) an open surface S bounded by a closed curve C, varies with time then a voltage v around C exists”; specifically
v = -dΦ/dt
or, in integral form,
∫cE・dl = -d(∫s B・dS)/dt for a plane area S and B normal to S
Thus if B varies with time there must be a non-zero E present, or, a changing magnetic field generates an electric field.
The minus sign in the equation above indicates Lenz’s Law, namely “the voltage induced by a changing flux has a polarity such that the current established in a closed path gives rise to a flux which opposes the change in flux”.
In the special case of a conductor moving through a time-invariant magnetic field, the induced polarity is such that the conductor experiences magnetic forces which oppose its motion.