


Rough Notes:
NUMBER SYMBOLISM
"But thou hast arranged all things by measure and number and weight."
Book of Wisdom of Solomon, from the OT Apocrypha., XI, 20.
Elementary Number Symbolism
The Pythagoreans were not the only ones who gave symbolic meaning to numbers. According to Vincent Hopper, "nothing in the history of number symbolism is so striking as the unanimity of all ages and climates in regard to the meanings of a few number symbols." He refers to this as elementary number symbolism.
In addition, we'll include numbers from mythology, astrology, and the Old Testament, which is loaded with symbolic numbers. We'll cover the New Testament and Christian number symbolism in a later unit.
We'll be able to connect some of the numbers used symbolically to larger ideas, but others will seem completely arbitrary. For those, our only justification in mentioning them is their repeated use as art motifs, and whose recognition may help us to understand a work of art.
Numero Uno
| HILDEGARD: Man in Sapphire Blue Fox, p. 22 |
According to Hopper, the first advance towards counting is with the use of words for one and for many, the differentiation from the self from the group. We still say numero uno to speak of ourselves.
One - the first - the greatest - the beginning - is usually identified with the Creator. In the beginning God created . . ., so in the beginning there was only one.
Two & Duality
| Slide 4-3: Janus Cayley. Classical Myths in English Literature. Boston: Ginn 1893 p. 89 |
The number two appears to always have carried with it the idea of duality, of opposites and mutual antithesis, as we've seen with the Pythagoreans. Here is the Greek god Janus, for whom January is named. He sees both ways, both inwards and outwards, and has the wisdom of both past and future.
| Slide 4-4: DÜRER: Adam and Eve Dürer, Albrecht. The Complete Engravings, Etchings and Drypoints. Ed. By Walter Strauss. NY: Dover, 1972. |
Aristotle said, "most human things go in pairs." We have many sets of dualities, like night and day, hot, cold, etc. and especially male, female.
| sun | moon |
| light | darkness |
| heat | cold |
| fire | water |
| day | night |
| active | passive |
| male | female |
Yin and Yang
The Chinese believed that heaven and earth produced everything by the interaction of opposites called Yang and Yin, the masculine Yang and the feminine Yin, just as offspring are the result of the interaction of a male and a female parent.
Famous Trios
Three represents the triad of family; male, female, and child; beginning, middle, and end; birth, life, and death.
Of two things we say both; of three things we say all.
Hopper writes that a single occurance is of no statistical significance, a second occupance might be just coincidence, but a third occurrence gives the event the impress of law, thus the Gypsy belief that if a dream comes three times it is certain to be true.
Egyptian Sun Gods
| Slide 4-7: Egyptian Deities New International Encyclopedia. NY: Dodd, 1917. Volume 7, p. 529 |
Three became the most universal number of deity, like the Holy Trinity that we'll cover in a later unit. There were three primary gods of Babylon Anu, Bel, and Earepresenting heaven, earth, and the abyss.
Sun worship is one of the most primitive forms of religion, and early man sometimes distinguished between rising, midday, and setting sun. The Egyptians, for example, divided the sun god into three deities:
| Horus, rising sun | Ra or Rê, midday sun | Osiris, old setting sun |
Triple Goddess
| Slide 4-8: White Goddess Graves Cover |
Just as three positions of the sun are represented by three deities, so with the moon.
Robert Graves writes about the White Goddess,
. . . the triple goddess of the New, Full, and Old Moon,
. . . goddess of Birth, Love, and Death . . .
. . . beautiful, generous, fickle, wise, implacable.
Three Fates
| Slide 4-10: MICHELANGELO.Three Fates Cayley. Classical Myths in English Literature. Boston: Ginn 1893 p. 72 |
There are lots of trios of women in mythology and in art . . .
Recall from our unit on Music of the Spheres that the circles of heaven turned and on each was a siren, each singing a single note. Plato, Republic, Chap XL, says that on the circles were the three fates, daughters of Necessity, the three sisters that controlled destiny, chanting to the Sirens' music. Lacheses of things past, Clotho of things present, Atropos of things to come, like the three ghosts in Dickens' A Christmas Story.
The length of someone's life was determined by the length of a single thread. Clotho held the spool, Lachesis pulled the thread, Atropos snipped.
Three Sirens
Plato's sirens are not to be confused with the three sirens, sea nymphs in the Mediterranean whose singing lead men to their deaths on the rocks. In the Odyssey, Odysseus resists them by tying himself to the mast and plugging the sailor's ears with wax. They symbolize the hazards faced by early mariners.
Three Witches
| Slide 4-11: FUSELI: Three Witches Clark, Kenneth, The Romantic Rebellion. NY. Harper, 1972. |
Recall the famous lines from Macbeth,
Double, double, toil and trouble; Fire burn and cauldron bubble.
They appear to be making hot soup for lunch, and Shakespeare even gives the recipe, poison'd entrails, selter'd venom, fillet of fenny snake, eye of newt, toe of frog . . . and much more.
Three Furies
These three lovelies are sometimes called Resentful, Relentless, and Avenger. Their heads were covered with serpents and they breathed vengeance and pestilence. They were often found in the company of Mars, god of war.
Three Graces
| Slide 4-13: RAPHAEL: The Three Graces, 1505-6. Fisher, Sally. The Square Halo. NY: Abrams, 1995. p. 166 |
A more appealing trio of women is The Three Graces, sometimes called Splendor, Mirth, and Good Cheer, or Beauty, Gentleness, and Friendship. They were often shown with Venus, the nine Muses, and Apollo. The three graces is a very popular art motif, with involved iconography, but might have been just an excuse for artists to portray nude women.
Judgement of Paris
| Slide 4-19: RUBENS:Judgement of Paris American Library Color Slide Company Slide # 863 |
A trio of women is also the subject of another favorite art motif, the Judgement of Paris. Paris was the son of the king and queen of Troy. They heard a prophecy that Paris would be the ruin of Troy so put him on Mount Ida where he was brought up by shepherds.
Years later the three goddesses, Hera, Athena, and Aphrodite, were at a wedding where someone tossed a golden apple into the crowd, inscribed "To the Fairest." All three wanted it and asked Zeus to decide, but he was too smart to get involved. He packed them all off to Mount Ida for Paris to make the decision.
Hera and Athena offered him riches, fame, empire, and military glory, but when Aphrodite bribed him with the offer of Helen, whom, he voted for Aphrodite, even though Helen was already married and Paris himself was in love with a nymph. What's more, Paris had to go and abduct Helen, which started the Trojan War.
This motif was also used as an allegory representing a choice between the active life and the sensuous one.
Earthly Fours
The number four is associated with the earth in many ways.
Four Ages of the World
Ovid writes of the Four Ages of the World:
Gold, the first, free of fear and conflict
Silver, the second, where man had to seek shelter
Bronze, the third, aggressive but not yet entirely evil
Iron, the fourth, with treachery, violence, greed deceit, and war.Four Continents
| Africa | Nile | crocodile, lion, snake, elephant |
| Americas | Plate | hunter with feathered headpiece |
| Asia | Ganges | camel, rhino, elephant |
| Europe | Nile | bull or horse |
| Slide 4-26: TITIAN: Rape of Europac.1560. Hartt, Frederic. Italian Renaissance Art. NY: Abrams, 1994. p. 609 |
| Slide 4-27: GIORDANO: Rape of Europa, 1686 Janson, H. W. History of Art. Fifth Edition. NY: Abrams, 1995. p. 557 |
The Rape of Europa is a very popular art motif.
Zeus fell in love with the maiden Europa, disguised himself as a bull, fitting for this horniest of Gods, and abducted her to Crete. She eventually gave birth to the continent of Europe.
Four Cardinal Virtues
| Slide 4-29: ANDREA DELLA ROBBIA: Allegory of Prudence Fisher, Sally. The Square Halo. NY: Abrams, 1995. c. 1475. p. 165 |
Plato, in his Republic mentions four virtues, Prudence (or Wisdom), Fortitude (or Courage), Temperance, and Justice. These are called the four cardinal virtues to distinguish them from the three Ecclesiastical virtues we'll see later in the New Testament.
Number Symbolism
in the Old Testament
To elementary number symbolism we add the Old Testament, in which everything is numbered. Sometimes the numbers have symbolic meaning, but the numbers are often used, it seems, just to make the narrative more concrete, saying, for example, that "Solomon built a house 100 cubits long"instead of "Solomon built a really long house."
Umberto Eco says that much number symbolism can be attributed to the passage from the Book of Wisdom of Solomon, from the OT Apocrypha. XI, 20.
Four Cardinal Points
The Old Testament has many references to the four cardinal directions, such as in Isaiah 11, 12:
"And he shall ... gather together the dispersed of Judah from the four corners of the earth."
and Ezekiel 7, 2:
"An end, the end is come upon the four corners of the land"Four Winds
| Slide 4-25: Kitzinger, Ernst. The Art of Byzantium and the Medieval West. Bloomington: Indiana, 1976. p. 333 |
The invention of the four winds is a simple enough addition. In Jeremiah 49, 36 we read
"I bring the four winds from the four quarters of heaven, and will scatter them toward all those winds"
From Virgil's Aeneid we have Aeolus, King of the Winds, who lived on an island just north of Sicily, who ruled the four winds:
Boreas, the north wind (Latin, Aquilo)
Zephyr, the west wing (Latin Favonius)
Notus, the south wind (Latin Auster)
Eurus, the east wind (same in Latin)
Four Rivers
Four rivers are mentioned in the Old Testament, Gen 2, 10:
" And a river went out of Eden ... and parted ... into four heads.
The . . . first [is] Pison ... which compasses the whole land of Havilah ...
the second [is] Gihon ... that compasses the whole land of Ethiopia ...
the third [is] Hiddekel ... that goes toward the east of Assyria ...
and the fourth [is] Euphrates that goes eastward to Assyria."
Four Rivers of Hell
| Slide 4-28: Aeneas and the Sibyl enter Charon's boat. Hamilton, Edith. Mythology. NY: Mentor, 1942, p. 227 |
The four rivers of Hades, Acheron, Styx, Phlegethon, and Cocytus, are not from the Old Testament, but play an important role in Plato's Phaedo, Dante's Inferno. and Virgil's Aeneid. In this picture, Aeneas and the Sibyl enter Charon's boat to cross at the junction of the Acheron and the Cocytus.
Astrological Numbers
| Slide 4-21: Phases of the Moon "Maps of Heavens." The British Library |
Another major source of number symbolism is Astrology, an ancient practice that seemed to develop independently in different civilizations.
The Chaldeans, who lived in Babylonia (now Iraq), developed astrology as early as 3000 B.C.E., and the Chinese were practicing astrology by 2000 BC. Astrology was known in ancient India and by the Maya of Central America. By the 500s BC, astrology had spread to Greece, where Pythagoras and Plato used it into their study of religion and astronomy.
It is certainly clear that certain astronomical bodies, particularly the sun, affected the change of seasons and the success of crops. So its not a big leap to assume that the movements of other bodies such as the planets affected or represented additional aspects of life. They also gave our notions of time, from the daily cycle of night and day, the lunar cycle of 28 days, giving the month, subdivided into the four phases of the moon, and the yearly cycle of 12 lunar cycles or about 360 daily cycles.
Four Seasons
| Slide 4-22: Hades & Persephone Hamilton, Edith. Mythology. NY: Mentor, 1942 p. 22 |
In Greek mythology, the seasons came about when Demeter's daughter, Persephone was abducted to the underworld by Hades. There followed an awful flap, too involved to relate here, but they finally cut a deal where Persephone spent half the year in the underworld, which time became autumn and winter, and half above ground, which became spring and summer.
Four Divisions of the Day
| Slide 4-23: MICHELANGELO: Sculptures in Medici Chapel, closeup of Notte Canaday, John.Masterpieces by Michelangelo. NY: Crown, 1979. p. 95 |
The division of the day into 4 periods, dawn, day, evening, and night, is here represented by Michelangelo, in the Medici Chapel.
Four Cardinal Points
| Slide 4-24: Compass Rose Calter Photo |
The movements of celestial bodies may also have led to Four becoming identified with the four directions, toward the sunrise, towards the sunset, and the two directions perpendicular to these.
Thus four is the number of the cardinal points, N, S, E, W, and the directions in which a person can move; right, left, forward, back.
Celestial Sevens
| Slide 4-35: VEDDER: The Pleides Cayley. Classical Myths in English Literature. Boston: Ginn 1893 p. 146 |
Seven is one of the main astrological numbers.
- Since 4 lunar phases made a complete lunar cycle of 28 days, each phase was 7 days, which defines the week.
- There are seven stars in the Pleides.
Many a night I saw the Pleides, rising thro' the mellow shade, Glitter like a swarm of fireflies tangled in a silver braid.
From Locksley Hall by Alfred, Lord Tennyson (1809-92)
| Slide 4-36: Big Dipper National Geographic Map |
- There are seven stars in the Big Dipper, the most prominent of the "indestructible" stars, the circumpolar.
From Homer's Iliad we have; ". . . and the bear, which revolves in its place and watches Orion, and alone of [the stars] never takes a bath in the ocean."
- There are seven colors of the rainbow: red, orange, yellow, green, blue, indigo, violet
We'll have more about the rainbow as an art motif later.
Planets
The ancient world knew of seven "planets" and identified them with the days of the week.
| Day | Planet |
| Sunday | Sun |
| Monday | Moon |
| Tuesday | Mars |
| Wednesday | Mercury |
| Thursday | Jupiter |
| Friday | Venus |
| Saturday | Saturn |
Wisdom
Seven is often used as a number of wisdom. From the Old Testament, Proverbs 9:1:
"Wisdom hath builded her house, she hath hewn out her seven pillars"The Flood
| Slide 4-37: DORE: The Deluge O. M. Dunham. "Bible Gallery," 1880 |
Other Sevens from the Old Testament include the great flood. Noah had seven days to prepare before the flood. He was commanded to take seven pair of clean beasts and birds.
"Of every clean beast thou shalt take to thee by sevens, the male and the female: and of beasts that are not clean by two, the male and the female."
Clean and unclean spelled out in Leviticus Chapter 11, where clean meant ritually pure, similar to what we consider Kosher.
The Creation
| Slide 4-38: MICHELANGELO: Creation of the Sun, Moon, and Vegetation Canaday, John.Masterpieces by Michelangelo. NY: Crown, 1979. p. 17 |
Other Sevens from the Old Testament include the Seven acts of creation;
- light, 2. firmament, 3. plants, 4. heavenly bodies, 5. fish & fowl, 6. animals & humans, 7. rest.
Sabbatical & Jubilee
The notion that the seventh day was for rest led to the adoption of the weekly Sabbath as a day of rest. But other sacred times of the calendar were based on seven, the seventh or sabbatical year.
Leviticus 25: 1-4: And . . . then shall the land keep a Sabbath . . . Six years shall you sow your field, and prune thy vineyard, and gather fruit. But the seventh year shall be a Sabbath of rest unto the land you shall neither sow your field, nor prune your vineyard.
and the Jubilee year.
Leviticus 25, 8- 11: And you shall number seven Sabbaths of years unto thee, seven times seven years; Then shalt thou cause the trumpet of the jubilee to sound . . . And ye shall hallow the fiftieth year, and proclaim liberty throughout the land it shall be a jubile unto you; and ye shall return every man unto his possession, and ye shall return every man unto his family. . . . ye shall not sow, neither reap that which groweth of itself in it, nor gather [the grapes]. . .
Menorah
| Slide 4-39: Menorah Keller, Sharon. The Jews: A Treasury of Art and Literature. NY: Levin Assoc. 1992. |
Seven also numbers the days of Passover and the branches of the menorah
Exodus 25, 31-37: "And thou shalt make a candlestick [of] pure gold . . .. . six branches shall come out of the sides of it; three branches . . . out of the one side, . . . and three branches out of the other side . . . Three bowls made like unto almonds . . . in one branch. . . and three bowls made like almonds in the other branch. . . . And you shall make the seven lamps thereof."
|
Slide 4-40: Menorah, lit Calter Photo |
Robert Graves gives the menorah cosmic significance by comparing the seven flames to the seven planets. He cites Zechariah 4:1-10,
"And the angel . . . came again, and waked me, . . . And he said to me, What seest thou? And I said, I have seen, . . . a candlestick all of gold, with its bowl upon the top of it, and its seven lamps thereon; . . . [these are] the eyes of Jehovah, which run to and fro through the whole earth."
| Slide 4-41: Menorah, lit in a dark room Calter Photo |
Graves takes the seven eyes to mean the seven planets.
Chanukah Candlestick
| Slide 4-43: Silver Menorah, Prague, 1860 Levin, Hugh, Associates. Jewish Calendar, 1997. |
In contrast to the Menorah of Exodus with seven candles is the Chanukah menorah with eight candles, which celebrates a miracle. The story is that when the Temple in Jerusalem was rededicated after the war of the Macabees (167-160 B.C.E.) and after being desecrated by Antiochus Epiphanes, only a small amount of oil was found to light the menorah but it lasted for eight days.
A ninth candle, the Shamesh, is used to light the other eight, one night at a time, for the eight days of Chanukah, the festival of lights occurring near the winter solstice.
Ten Digits
Being the number of fingers or toes, ten became the base of the decimal number system. It is the number of completeness or finality.
With ten as complete, nine comes into prominence as almost complete. Troy was besieged for 9 days and fell on the tenth. Odysseus wandered for 9 years and arrived home on the tenth.
Ten Commandments
From the Old Testament we have, of course, the ten commandments or Decalogue. The Old Testament also describes Tithing, to give a tenth part of one's income.
Twelve and the Zodiac
| Slide 4-48: Zodiac Pavement Keller, Sharon. The Jews: A Treasury of Art and Literature. NY: Levin Assoc. 1992. p.20 |
Twelve is one of the big numbers in astrology because twelve complete lunar cycles takes approximately one year. Each month was eventually identified with a sign of the zodiac, which is believed to have originated in Mesopotamia as early as 2000 BC. The Greeks adopted the symbols from the Babylonians and passed them on to the other ancient civilizations.
The Egyptians assigned other names and symbols to the zodiacal divisions. The Chinese also adopted the 12-fold division, but called the signs rat, ox, tiger, hare, dragon, serpent, horse, sheep, monkey, hen, dog, and pig. The Aztecs independently devised a similar system.
Twelve thus symbolized a complete cycle; and twelve was also used to divide the day and also the night.
Twelve Gods of Olympus
Slide 4-49: MANTEGNA: Parnassus American Library Color Slide Co. Inc. Slide #7507
Twelve is the number of Gods on Mount Olympus:
The Four siblings
| 1. Zeus | Jupiter | supreme ruler |
| 2. Poseidon | Neptune | ruler of the sea |
| 3. Hades | Pluto | ruler of the underworld |
| 4. Hestia | Vesta | virgin. hearth & home |
| 5. Hera | Juno | Zeus' wife |
The Children of Zeus
| 6. Ares | Mars | war |
| 7. Pallas Athena | Minerva | virgin |
| 8. Hephaestus | Vulcan | fire, forge |
| 9. Phoebus | Apollo | Apollo beautiful |
| 10. Artemis | Diana | huntress, virgin |
| 11. Hermes | Mercury | messenger |
| 12. Aphrodite | Venus | love & beauty, mother of Aeneus |
But, curiously, the twelve Olympians are not all associated with the 12 signs of the zodiac.
Twelve Labors of Hercules
| Slide 4-50: POLLAIUOLO: Hercules and Antaeus Janson, H. W. History of Art. Fifth Edition. NY: Abrams, 1995. p. 466 |
Twelve is associated with Hercules, a very popular art motif. The Renaissance artist Pollaiuolo, for example, did an entire series of paintings on Hercules.
| Slide 4-51: Herculaneum Calter Photo |
Hercules even had a city named for him, Herculaneum, destroyed in 79 AD by the same eruption of Vesuvius that buried Pompeii. The Italian city of Ercolano still bears his name.
Fatal Forties
Forty is the number of trial and privation, possibly starting when the Babylonians observed the forty-day disappearance of the Pleides which coincided with the rainy season, storms and floods, trial, danger. The Pleides' return marked the start of the New Year Festival. Other negative associations for forty are:
- 40 years of Hebrew wandering in the desert
- 40 days and nights of the great flood.
- 40 years of Philistine dominion over Israel
- 40 days of Moses on Sinai
- 40 days of Elijah's journey
- 40 days of mourning for Jacob
- 40 days, and Nineveh shall be overthrown, said Jonah.
- 40 days of Lent, the period of fasting, self-denial, and penitence traditionally observed by Christians in preparation for Easter.
- 40 day period of isolation in the Roman port, which survives in the wordquarantine.
Summary
Tabulating some of our number symbolism, we have:
| One | Self, Deity, Source of all Numbers |
| Two | Duality, Defect |
| Three | All, Best, Holy, First Triangular |
| Four | Astrological Number, Earth, First Square |
| Seven | Astrological, Steps to Wisdom and Virtue |
| Ten | Completeness, Finality, Perfection |
| Twelve | Zodiac, A Complete Cycle |
| Forty | Trial and Privation |
We may laugh now at some of the meanings given to numbers, but how many of us would be willing to stay in room 13 or on the 13th floor on Friday the 13th?
We're not finished with number symbolism. We'll cover those associated with the New Testament, Christianity, and the Middle Ages later.
Keep in mind that we're on shaky ground here. Much of this material is speculation, without any real proof, and is full of contradictions.
So why did we do this? We're not so much interested in the numbers themselves but we are looking for frequently used art motifs. Further, seeing how the ancients viewed numbers will help us get into the right frame of mind to understand how they viewed geometric figures, triangles, squares, octagons, and that's the subject of our next unit.
Polygons, Tilings,
&
Sacred Geometry

Slide 5-1: Pompeii pavement
Calter photo
In the last unit, Number Symbolism, we saw that in the ancient world certain numbers had symbolic meaning, aside from their ordinary use for counting or calculating.
In this unit we'll show that the plane figures, the polygons, triangles, squares, hexagons, and so forth, were related to the numbers (three and the triangle, for example), were thought of in a similar way, and in fact, carried even more emotional baggage than the numbers themselves, because they were visual. This takes us into the realm of Sacred Geometry.
For now we'll do the polygons directly related to the Pythagoreans; the equilateral triangle (Sacred tetractys), hexagon, triangular numbers, and pentagram. We'll also introduce tilings, the art of covering a plane surface with polygons.
| Outline: | Polygons |
| EquilateralTriangle | |
| Tilings | |
| Hexagon & Hexagram | |
| Pentagon & Pentagram | |
| Golden Triangle | |
| Conclusion | |
| Reading | |
| Projects |

Slide 5-23: Design at Pompeii
Calter photo
In the last unit, Number Symbolism we saw that in the ancient world certain numbers had symbolic meaning, aside from their ordinary use for counting or calculating. But each number can be associated with a plane figure, or polygon (Three and the Triangle, for example).
In this unit we'll see that each of these polygons also had symbolic meaning and appear in art motifs and architectural details, and some can be classified as sacred geometry.
A polygon is a plane figure bounded by straight lines, called the sides of the polygon.
From the Greek poly = many and gon = angle
The sides intersect at points called the vertices. The angle between two sides is called an interior angle or vertex angle.
Regular Polygons
A regular polygon is one in which all the sides and interior angles are equal.
Polygons vs. Polygrams
A polygram can be drawn by connecting the vertices of a polgon. Pentagon & Pentagram, hexagon & hexagram, octagon & octograms
 |
Slide 5-2: Tablet in School of Athens, showing Tetractys Bouleau |
There are, of course, an infinite number of regular polygons, but we'll just discuss those with sides from three to eight. In this unit we'll cover just those with 3, 5, and 6 sides. We'll start with the simplest of all regular polygons, the equilateral triangle.
Sacred Tetractys
The Pythagoreans were particularly interested in this polygon because each triangular number forms an equilateral triangle. One special triangular number is the triangular number for what they called the decad, or ten, the sacred tetractys.
Ten is important because it is, of course, the number of fingers. The tetractys became a symbol of the Pythagorean brotherhood. We've seen it before in the School of Athens.
Trianglular Architectural Features

Slide 8-11: Church window in Quebec
In architecture, triangular windows are common in churches, perhaps representing the trinity.
Triskelion, Trefoil, Triquerta
Other three-branched or three-comered designs include the triskelion.

Slide 5-3: Greek Triskelion: Victory and Progress
Lehner, Ernst. Symbols, Signs & Signets. NY: Dover, 1950 p. 85

Slide 5-4: Irish Triskelions from Book of Durrow.
Met. Museum of Art. Treasures of Early Irish Art. NY: Met. 1977
Its a design that I liked so much I used it for one of my own pieces.
 |
Slide 5-5: Calter carving Mandala II Calter photo |
 |
Slide 5-6: Closeup of wheel Calter photo |
 |
Slide 5-7: Pompeii Tiling with equilateral triangles Calter photo |
Tilings or tesselations refers to the complete covering of a plane surface by tiles. There are all sorts of tilings, some of which we'll cover later. For now, lets do the simplest kind, called a regular tiling, that is, tiling with regular polygons.
This is opposed to semiregular tilings like the Getty pavement shown here.
 |
Slide 5-8: Getty Pavement Calter photo |
The equilateral triangle is one of the three regular polygons that tile a plane. the other two being the square and hexagon.
 |
Slide 5-15: Plate with Star of David Keller, Sharon. The Jews: A Treasury of Art and Literature. NY: Levin Assoc. 1992 |
Hexagonal Tilings
Our next polygon is the hexagon, closely related to the equilateral triangle
The hexagon is a favorite shape for tilings, as in these Islamic designs, which are not regular tilings, because they use more than one shape.

Slide 5-9: Islamic Tiling Patterns
El-Said, Issam, et al. Geometric Concepts in Islamic Art. Palo Alto: Seymour, 1976. p. 54
But, as we saw, the hexagon is one of the three regular polygons will make a regular tiling.
An Illusion
The hexagon is sometimes used to create the illusion of a cube by connecting every other vertex to the center, forming three diamonds, and shading each diamond differently.
 |
Slide 5-10: Basket Calter photo |
 |
Slide 5-11: Pavement, Ducal Palace, Mantua Calter photo |
The Hexagon in Nature
The hexagon is found in nature in the honeycomb, and some crystals such as basalt, and of course, in snowflakes.
 |
Slide 5-12: Snowflakes Bentley, W. A. Snow Crystals.NY: Dover, 1962. |
Six-Petalled Rose
The hexagon is popular in architectural decoration partly because it is so easy to draw. In fact, these are rusty-compass constructions, which could have been made with a forked stick.
Six circles will fit around a seventh, of the same diameter, dividing the circumference into 6 equal parts, and the radius of a circle exactly divides the circumference into six parts, giving a six petalled rose.
 |
Slide 5-13: Moses Cupola. S. Marco, Venice Demus, Otto. The Mosaic Decoration of San Marco, Venice. Chicago: U. Chicago, 1988. plate 60. |
Hexagon vs. Hexagram
Connecting alternate points of a hexagon gives a hexagram, a six-pointed star, usually called the Star of David, found in the flag of Israel.

Slide 5-14: Star of David on Silver bowl from Damascus.
Jewish Museum (New York, N.Y.), Treasures of the Jewish Museum. NY: Universe, 1986. p. 61
Solomon's Seal
The hexagrarn is also called a Solomon's Seal. Joseph Campbell says that King Solomon used this seal to imprison monsters & giants into jars.
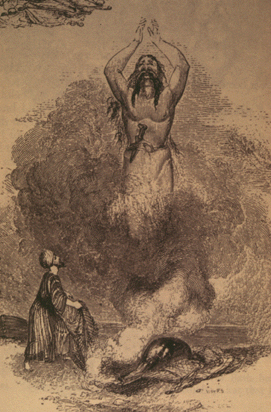 |
Slide 5-17: The genii emerging. Burton, Richard. The Arabian nights entertainments.Ipswich : Limited Editions Club, 1954. |
The U.S. Great Seal
 |
Slide 5-20: Seal on Dollar Bill Calter photo |
The hexagrarn can also be viewed as two overlapping Pythagorean tetractys.
Joseph Campbell writes; In the Great Seal of the U.S. there are two of these interlocking triangles. We have thirteen points, for our original thirteen states, and six apexes: one above, one below, andfour to thefour quarters. The sense of this might be thalftom above or below, orftom any point of the compass, the creative word may be heard, which is the great thesis of democracy.
- The Power of Myth. p.27
Hexagonal Designs in Architecture
Hexagonal designs are common in ancient architecture, such as this church window in Quebec.
 |
Slide 5-22: Church Window in Quebec Calter photo |
This marvelous design is at Pompeii. It is made up of a central hexagon surrounded by squares, equilateral triangles, and rhombi.

Slide: 5-23. Design at Pompeii
Calter photo

Slide 5-24: Design on Pisa Duomo
Calter photo
This hexagram is one of countless designs on the Duomo in Pisa.
 |
Slide 5-26: Pentagram from grave marker Calter photo |
The Pentagram was used as used as a sign of salutaton by the Pythagoreans, its construction supposed to have been a jealously guarded secret. Hippocrates of Chios is reported to have been kicked out of the group for having divulged the construction of the pentagram.
The pentagram is also called the Pentalpha, for it can be thought of as constructed of five A's.
Euclid's Constructions of the Pentagon
Euclid gives two constructions in Book IV, as Propositions 11 & 12. According to the translator T.L. Heath, these methods were probably developed by the Pythagoreans.
Medieval Method of Construction
Supposedly this construction was one of the secrets of Medieval Mason's guilds. It can be found in Bouleau p. 64.
Durer's Construction of the Pentagon
Another method of construction is given in Duret's "Instruction in the Measurement with the Compass and Ruler of Lines, Surfaces and Solids," 1525.
Its the same construction as given in Geometria Deutsch, a German book of applied geometry for stonemasons and
Golden Ratios in the Pentagram and Pentagon
The pentagon and pentagram are also interesting because they are loaded with Golden ratios, as shown in Boles p.48.

Slide 5-28: Emmer, plate F3
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993.
The Golden Triangle
A golden triangle
also called the sublime triangle, is an isoceles triangle whose ratio of leg to base is the golden ratio.
It is also an isoceles triangle whose ratio of base to leg is the golden ratio, so there are two types: Type I, acute, and type II, obtuse.
A pentagon can be subdivided into two obtuse and one acute golden triangle.
Euclid's Construction
Euclid shows how to construct a golden triangle. Book IV, Proposition 10 states, "To construct an isoceles triangle having each of the angles at the base the double of the remaining one."
Penrose Tilings
 |
Slide: 5-27: Penrose Tilings. Kappraff, Jay. Connections: The Geometric Bridge between Art & Science.NY: McGraw, 1990. p. 195 |
One place that the golden triangle appears is in the Penrose Tiling, invented by Roger Penrose, in the late seventies. The curious thing about these tilings is they use only two kinds of tiles, and will tile a plane without repeating the pattern.
Making a Penrose TilingA Penrose tiling is made of two kinds of tiles, called kites and darts. A kite is made from two acute golden triangles and a dart from two obtuse golden triangles, as shown above.
 |
Slide 5-29: NCTM Cover |
So we covered the triangle, pentagon, and hexagon, with sides 3, 5, and 6. We'll cover the square and octagon in a later unit.
Its clear that these figures, being visual, carried even more powerful emotional baggage than the numbers they represent.
Next time we'll again talk about polygons, in particular the triangle. But I won't waste your time with some insignificant and trivial fact about the triangle, but will show that, according to Plato, triangles form the basic building block of the entire universe!
The PLATONIC SOLIDS
"Let no one destitute of geometry enter my doors."
Plato (c. 427 - 347 B.C.E.)

American Catalgo, p. 126, #21061. Fresco, Vatican, Stanza della Signurata, the Pope's Private Library
We now move forward in time about 150 years, still staying in Greece, from Pythagoras to Plato, himself a Pythagorean.
In our last unit we studied some polygons, and I said that one of these, the triangle, was thought by Plato to be the building block of the universe. He presented that idea and others about creation, such as the universe being created to resemble a geometric progression, in one of his books, the Timaeus.
In the Timaeus, we'll see how Plato describes how triangles make up five solids, now called the Platonic Solids, and how these solids make up the four elements and heaven. We'll look at regular polyhedra in general, and see why only five are possible.
Finally we'll see how the Platonic solids were used as art motifs even before Plato, how they were used later, and how the served to tie together three Renaissance mathematicians and artists, Piero della Francesca, Luca Pacioli, and Leonardo da Vinci.
| Outline: | Plato |
| The Timaeus | |
| Music of the Spheres | |
| The Elements | |
| The Platonic Solids | |
| Polyhedra | |
| Polyhedra in Art & Architecture | |
| Summary |
 |
Slide 6-2: RAPHAEL: School of Athens. Center section |
Profile: Plato (c.427-347 B.C.E.) was born to an aristocratic family in Athens. As a young man Plato had political ambitions, but he became disillusioned by the political leadership in Athens. He eventually became a disciple of Socrates, accepting his basic philosophy and dialectical style of debate, the pursuit of truth through questions, answers, and additional questions. Plato witnessed the death of Socrates at the hands of the Athenian democracy in 399 BC. In Raphael's School of Athens we see Socrates prone, with cup nearby.
Plato's most prominent student was Aristotle, shown here with Plato in Raphael'sSchool of Athens, Aristotle holiding his Ethics and Plato with his Timaeus.
Plato's Academy
In 387 BCE Plato founded an Academy in Athens, often described as the first university. It provided a comprehensive curriculum, including astronomy, biology, mathematics, political theory, and philosophy.
Plato's final years were spent lecturing at his Academy and writing. He died at about the age of 80 in Athens in 348 or 347.
Over the doors to his academy were the words

meaning, "Let no one destitute of geometry enter my doors."
Plato on Art and Geometry
Although Plato loved geometry, he would not have been good at teaching a course in Art & Geometry because he had a low opinion of art. He taught that, since the world is a copy or image of the real, then a work of art is a copy of a copy, at third remove from reality.
He writes in his Republic(p. 603),
"... painting [and] ... the whole art of imitation is busy about a work which is far removed from the truth; ... and is its mistress and friend for no wholesome or true purpose. ... [it] is the worthless mistress of a worthless friend, and the parent of a worthless progeny."
But on geometry he wrote in his Republic (p. 527),
"[Geometry is] . . . persued for the sake of the knowledge of what eternally exists, and not of what comes for a moment into existence, and then perishes, ...
[it] must draw the soul towards truth and give the finishing touch to the philosophic spirit."
Plato left lots of writings. We've mentioned his Republic in our unit on number symbolism in which he gave the four cardinal virtues, but his love of geometry is especially evident in the Timaeus.
Written towards the end of Plato's life, c. 355 BCE, the Timaeus describes a conversation between Socrates, Plato's teacher, Critias, Plato's great grandfather, Hermocrates, a Sicilian statesman and soldier, and Timaeus, Pythagorean, philosopher, scientist, general, contemporary of Plato, and the inventor of the pulley. He was the first to distinguish between harmonic, arithmetic, and geometric progressions.
In this book, Timaeus does most the talking, with much homage to Pythagoras and echos of the harmony of the spheres, as he describes the geometric creation of the world.
Plato, through Timaeus, says that the creator made the world soul out of various ingredients, and formed it into a long strip. The strip was then marked out into intervals.
| First [the creator] took one portion from the whole | (1 unit) |
| and next a portion double the first | (2 unit) |
| a third portion half again as much as the second | (3 unit) |
| the fourth portion double the second | (4 unit) |
| the fifth three times the third | (9 unit) |
| the sixth eight times the first | (8 unit) |
| and the seventh 27 tmes the first | (27 unit) |
They give the seven integers; 1, 2, 3, 4, 8, 9, 27. These contain the monad, source of all numbers, the first even and first odd, and their squares and cubes.
Plato's Lambda
 |
Slide 8-72 : Arithmetic Personified as a Woman Lawlor, Robert. Sacred Geometry. NY: Thames & Hudson, 1982. p. 7. |
These seven numbers can be arranged as two progressions
Monad 1 Point
First even and odd 2 3 Line
Squares 4 9 Plane
Cubes 8 27 Solid
This is called Plato's Lambda, because it is shaped like the Greek letter lambda.
Divisions of the World Soul as Musical Intervals
Relating this to music, if we start at low C and lay off these intervals, we get 4 octaves plus a sixth. It doesn't yet look like a musical scale. But Plato goes on to fill in each interval with an arithmetic mean and a harmonic mean. Taking the first interval, from 1 to 2, for example,
Arithmetic mean = (1+2)/2 = 3/2
The Harmonic mean of two numbers is the reciprocal of the arithmetic mean of their reciprocals.
For 1 and 2, the reciprocals are 1 and 1/2, whose arithmetic mean is 1+ 1/2 ÷ 2 or 3/4. Thus,
Harmonic mean = 4/3
Thus we get the fourth or 4/3, and the fifth or 3/2, the same intervals found pleasing by the Pythagoreans. Further, they are made up of the first four numbers 1, 2, 3, 4 of the tetractys.
Filling in the Gaps
He took the interval between the fourth and the fifth as a full tone. It is
3/2 ÷ 4/3 = 3/2 x 3/4 = 9/8
Plato then has his creator fill up the scale with intervals of 9/8, the tone. This leaves intervals of 256/243 as remainders, equal to the half tone.
Thus Plato has constructed the scale from arithmetic calculations alone, and not by experimenting with stretched strings to find out what sounded best, as did the Pythagoreans.
Project: Repeat Plato's calculations and see if you do indeed get a musical scale.
Forming the Celestial Circles
After marking the strip into these intervals, the creator then cut it lengthwise into two strips that are placed at an angle to each other and formed into circles. These correspond to the celestial equator and the ecliptic, the start of an armillary sphere.
 |
Slide 10-121: Armillary Sphere Turner, Gerard. Antique Scientific Instruments. Dorset: Blandford, 1980. p. 61 |
Recall our quotation from Plato's Republic, where, in the Myth of Er he wrote,
". . . Upon each of its circles stood a siren who was carried round with its movements, uttering the concords of a single scale." [Republic p. 354]
This is the origin of the expression, Music of the Spheres.
The idea tthat all things are composed of four primal elements: earth, air, fire, and water, is attributed to Empedocles (circa 493-433 BCE), Greek philosopher, statesman, and poet. He was born in Agrigentum (now Agrigento), Sicily, and was a disciple of Pythagoras and Parmenides.
Remember the opposite forces, Yin and Yang, male and female, whose interaction created everything in the universe? Empedocles thought that active and opposing forces, love and hate, or affinity and antipathy, act upon these elements, combining and separating them into infinitely varied forms.
He believed also that no change involving the creation of new matter is possible; only changes in the combinations of the four existing elements may occur.
Empedocles died about 6 years before Plato was born.
The Universe as a Geometric Progression
Plato deduces the need for the four elements. Timaeus, 31B-32C
1. First, we must have fire, to make the world visible, and earth to make it resistant to touch. These are the two extreme elements, fire belonging to heaven and earth to earth. He writes,
. . . it is necessary that nature should be visible and tangible ...
and nothing can be visible without fire or tangible without earth ...
2. But two cannot hold together without a third as a bond. [like glue]
. . . But it is impossible for two things to cohere without the intervention of a third ...
3. And the most perfect bond is the connued geometric proportion.
... [and] the most beautiful analogy is when in three numbers,
the middle is to the last as the first to the middle, . . . they become the same as to relation to each other.
4. But the primary bodies are solids, and must be represented by solid numbers (cubes).
To connect two plane numbers (squares) one mean is enough,
but to connect two solid numbers, two means are needed.
But if the universe were to have no depth, one medium would suffice to bind all the natures it contains. But . . . the world should be a solid, and solids are never harmonized by one, but always by two mediums.
Hence the Divinity placed water and air in the middle of fire and earth, fabricating them in the same ratio to each other; so that fire might be to air as air is to water and that water is to earth.
Thus the ratio is constant between successive elements, giving a geometric progression.
The Platonic Solids belong to the group of geometric figures called polyhedra.
A polyhedron is a solid bounded by plane polygons. The polygons are calledfaces; they intersect in edges, the points where three or more edges intersect are called vertices.
A regular polyhedron is one whose faces are identical regular polygons. Only five regular solids are possible
cube tetrahedron octahedron icosahedron dodecahedron
These have come to be known as the Platonic Solids
The Elements Linked to the Platonic Solids
Plato associates four of the Platonic Solid with the four elements. He writes,
We must proceed to distribute the figures [the solids] we have just described between fire, earth, water, and air. . .
Let us assign the cube to earth, for it is the most immobile of the four bodies and most retentive of shape
the least mobile of the remaining figures (icosahedron) to water
the most mobile (tetrahedron) to fire
the intermediate (octahedron) to air
Note that earth is associated with the cube, with its six square faces. This lent support to the notion of the foursquaredness of the earth.
The Cosmos
But there are five regular polyhedra and only four elements. Plato writes,
"There still remained a fifth construction, which the god used for embroidering the constellations on the whole heaven."
Plato's statement is vague, and he gives no further explanation. Later Greek philosophers assign the dodecahedron to the ether or heaven or the cosmos.
The dodecahedron has 12 faces, and our number symbolism associates 12 with the zodiac.
This might be Plato's meaning when he writes of "embroidering the constellations" on the dodecahedron.
Note that the 12 faces of the dodecahedron are pentagons. Recall that the pentagon contains the golden ratio. Perhaps this has something to do with equating this figure with the cosmos.
The Archimedian Solids
Slide 6-4: Archimedian Solids
Wenniger, Magnus J. Polyhedron Models for the Classroom. NCTM 1966. p. 7
Other sets of solids can be obtained from the Platonic Solids. We can get a set by cutting off the corners of the Platonic solids and get truncated polyhedra.
They are no longer regular; they are called semi -regular; all faces are regular polygons, but there is more than one polygon in a particular solid, and all vertices are identical.
These are also called the Archimedian Solids, named for Archimedes, (287-212) the Greek mathematician who lived in Syracusa on the lower right corner of Sicily.
Mini-Project: Make some Archimedian Solids.
Star Polyhedra
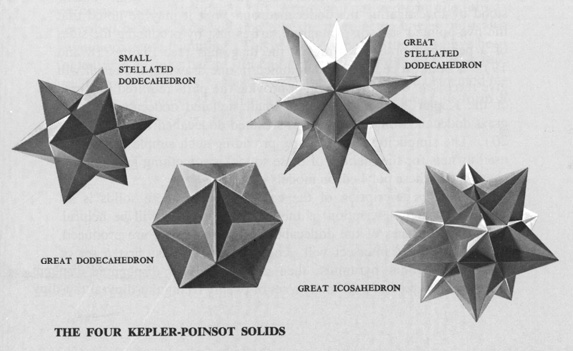
Slide 6-5: The Four Kepler-Poinsot Solids
Wenniger, Magnus J. Polyhedron Models for the Classroom. NCTM 1966. p. 11

Slide 6-6: Engraving from Harmonices Mundi, 1619.
Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993. p. 218
The second obvious way to get another set of solids is to extend the faces of each to form a star, giving the so-called Star Polyhedra.
Two star polyhedra were discovered by Poinsot in 1809. The others were discovered about 200 years before that by Johannes Kepler (1571-1630), the German astronomer and natural philosopher noted for formulating the three laws of planetary motion, now known as Kepler's laws, including the law that celestial bodies have elliptical, not circular orbits.
Mini-Project: Make some star polyhedra.
Polyhedra in Art & Architecture
Polyhedra are Nothing New
Polyhedra have served as art motifs from prehistoric times right up to the present.
 |
Slide 6-7: Pyramids Tompkins, Peter. Secrets of the Great Pyramid. NY: Harper, 1971. Cover |
The Egyptians, of course, knew of the tetrahedron, but also the octahedron, and cube. And there are icosahedral dice from the Ptolomaic dynasty in the British Museum, London.
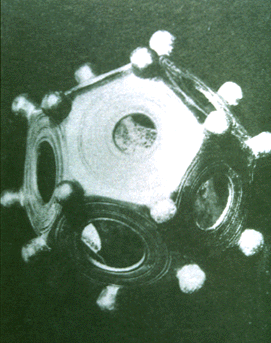 |
Slide 6-8: Etruscan Dodecahedron Emmer, Michele, Ed. The Visual Mind: Art and Mathematics.Cambridge: MIT Press, 1993. p. 216 |
There were Neolithic solids found in Scotland, and excavations near Padova have unearthed an Etruscan dodecahedron, c. 500 BCE, probably used as a toy.
Kepler
 |
Slide 3-6: Kepler's Model of Universe Lawlor, p. 106 |
In 1596 Kepler published a tract called The Cosmic Mystery in which he envisioned the universe as consisting of nested Platonic Solids whose inscribed spheres determine the orbits of the planets, all enclosed in a sphere representing the outer heaven. Of course, his observations did not fit this scheme. We'll encounter Kepler again in our unit on Celestial Themes in Art.
Polyhedra and Plagiarism in the Renaissance
 |
Slide 14-10 : JACOPO DE 'BARBERI: Luca Pacioli, c. 1499 |
This painting shows Fra Luca Pacioli and his student, Guidobaldo, Duke of Urbino. In the upper left is a rhombi-cuboctahedron, and on the table is a dodecahedron on top of a copy of Euclid's Elements.
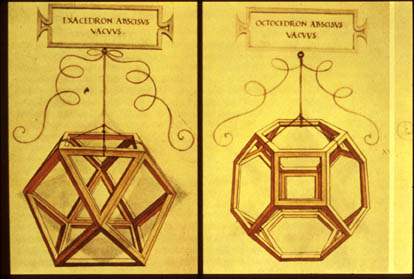 |
Slide 15-11 : Leonardo's Illustrations for Luca's book. Da Divina Proportione |
Luca Pacioli wrote a book called Da Divina Proportione (1509) which contained a section on the Platonic Solids and other solids, which has 60 plates of solids by none other than his student Leonardo da Vinci. We'll tell the whole story of how this material was stolen from Luca's teacher Piero della Francesca in our unit on Polyhedra and Plagiarism in the Renaissance.
Platonic Solids as Art Motifs
 |
Slide 6-12: UCELLO: Mosaic from San Marco Cathedral, Venice,1425-1430 plate J2 Emmer, Michele, Ed. The Visual Mind: Art and Mathematics.Cambridge: MIT Press, 1993. |
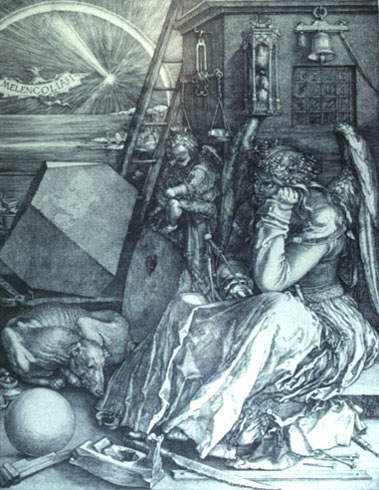 |
Slide 16-08: DURER:Melancolia I, 1514 citation |
Albrech Durer (1471-1528) had a keen interest in geometry, as we'll see in a later unit. This famous engraving shows an irregular polyhedron, as well as a sphere, a magic square, and compasses. People who have analyzed this polyhedron have decided that its actually a cube with opposite corners cut off.
 |
Slide 6-13: NEUFCHATEL, Nicolaus: Picture of Johannes Neudorfer and His Son,1561. Kemp, Martin. Leonardo on Painting. New Haven: Yale U. Press, 1989. p. 63 |
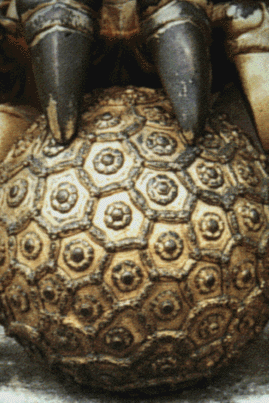 |
Slide 6-14: Gold-plated lion from the front of the Gate of Heavenly Purity, Closeup of Ball. Forbidden City, Beijing. From Qing Dynasty (1736-1796) |
This ball has hexagons interspersed with pentagons.
Polyhedra in Art in the Twentieth Century
|
|
Slides 6-15, 6-16, 6-17: Giacometti's Works Hohl, Reinhold. Alberto Giacometti. NY: Abrams, 1972. |
The Swiss artist Alberto Giacometti (1901-1966) often included polyhedra in his earlier surrealist works such as these two drawings and a sculpture.
 |
Slide 21-5: ESCHER:Stars 1948 (#123) |
We'll talk about M.C. Escher (1902-1972) in detail when we get to the 20th Century, but lets just peek at his 1948 engraving, Stars. Note the similarity between this polyhedron and Leonardo's illustrations for Pacioli's book.
 |
Slide 21-06: Escher contemplating his nested set of Platonic Solids citation |
Escher made a set of nested Platonic Solids. When he moved to a new studio he have away most of his belongings but took his beloved model.
Other Twentieth Century artists using polyhedra include Harriet Brisson, Paul Calter, and Lucio Saffaro.
 |
Slide 6-18:Truncated Close-Packing Octahedra, Rhombidodecahedra, and Cubes. Plexiglass, aluminum tubes, and nylon cord, 1976 Emmer, Michele, Ed. The Visual Mind: Art and Mathematics. Cambridge: MIT Press, 1993. plate B3 |
|
|
Slides 6-19, 6-20, 6-21: Platonic Solids Calter's Sorcerer's Circle |
 |
Slide 6-22: LUCIO SAFFARO:Platonic Forms.Computer graphic, 1989. Emmer, Michele, Ed. The Visual Mind: Art and Mathematics.Cambridge: MIT Press, 1993. plate A3 |
Project: Make a work of art featuring polyhedra.
So we've seen the origins of the Platonic Solids, starting even before Plato, and have briefly traced the influence of the polygons in art right up to the present.
We've also had a first look at some subjects we'll look at in more detail later.
For mathematical topics, we've briefly looked at sequences and series and the geometry of the polyhedra.





