


Rough Notes:
Octagram
Sun of Vergina – A Greek symbol
Το Αστέρι της Βεργίνας – Ένα Πανελλήνιο Σύμβολο
The Sun of Vergina is a symbol that was widely used by Ancient Greeks. It became famous due to the Macedonians who were using it as Symbol of the Argead Dynasty.
–The Royal house of Macedon:

The typical Sun of Vergina is a 16-pointed Sun. It can also be found in other styles: 12-pointed or 8-pointed. What was the meaning of this symbol?? –In the typical 16-pointed Sun , the 4 rays represent the 4 elements: Earth-Ocean-Fire-Air. The other 12 rays represent the 12 Gods of Olympus.You can see the explanation in the following animation :

–In every form, the Sun of Vergina symbolized Virginity:
Goddess Athena was a Virgin, so this Sun was associated with her. We can also find this symbol associated with Apollo. –All the versions (16,12 and 8-pointed Sun) are associated with another famous Greek symbol, the “Delphian Epsilon”, symbol of Apollo: 
The Sun of Vergina became common art design in coins, craters, wall-drawings etc LONG BEFORE the Macedonian royal house (the Argead Dynasty) used it. After the unification of the Greek (Hellenic) nation under the leadership of Alexander the Great, the Sun of Vergina became the symbol of the Hellenic Ethnogenesis.
In the following replies, you will be able to see some pieces of Ancient Greek art containing the Sun of Vergina, BEFORE THE RISE OF THE GREEK KINGDOM OF MACEDONIA. These sun symbols are found in various Greek places, apart from Macedonia. Moreover, there will be a small historical flashback, in order to see the evolution of this symbol throught the ages :
2000 BC:
This is the time where ancient Greeks first started using the Sun symbol. It was not standardized yet, it was a early form of the Sun of Vergina:

780BC:
The Sun of Vergina has been standardized. The following art work shows the destruction of Troy. We can clearly see the Sun symbol in the warrior’s hump. It was found in Mykonos island :

The following images are just a small sample, showing the wide usage of the Sun of Vergina in Greek Art:
Spartan Hoplite – 780 BC:

Spartan Amphoreus –
This vase can now be found in the Louvre Museum, Paris. 6th Century BC:

Exekias was a famous vase-painter and potter of ancient Athens. The scene on this page, from an amphora of the third quarter of the 6th century BC (now at the National Museum of Athens), is one of his most famous works. It is considered one of the finest surviving examples of ‘Black Figure’ vase painting.

Achilles and Ajax, two major Greek heroes of Homer’s Iliad are depicted here relaxing over a game of dice during a lull in the fighting. Achilles has just won; he has just thrown a ‘four’ while Ajax has to accept a ‘three’:
Third Quarter of the 6th century BC:

The cloaks of both these Homeric figures are studded with numerous 8-ray Sunbursts.
The return of Hephestus– 560 BC:

Athena and Hermes– 540 BC


Read more http://history-of-macedonia.com/2008/04/10/sun-of-vergina-a-greek-symbol/
| Regular octagram | |
|---|---|

A regular octagram
|
|
| Type | Regular star polygon |
| Edges and vertices | 8 |
| Schläfli symbol | {8/3} t{4/3} |
| Coxeter diagram | |
| Symmetry group | Dihedral (D8) |
| Internal angle(degrees) | 45° |
| Dual polygon | self |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
In geometry, an octagram is an eight-angled star polygon.
The name octagram combine a Greek numeral prefix, octa-, with the Greek suffix -gram. The -gram suffix derives from γραμμή (grammḗ) meaning "line".[1]
Contents
[hide]
Detail[edit]
In general, an octagram is any self-intersecting octagon (8-sided polygon).
The regular octagram is labeled by the Schläfli symbol {8/3}, which means an 8-sided star, connected by every third point.
Variations[edit]
These variations have a lower dihedral, Dih4, symmetry:
 Narrow 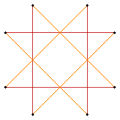 Wide (45 degree rotation) |
  Isotoxal |
 An old Flag of Chile contained this octagonal star geometry with edges removed. |
 The geometry can be adjusted so 3 edges cross at a single point, like the Auseklissymbol |
 An 8-point compass rose can be seen as an octagonal star, with 4 primary points, and 4 secondary points. |
The symbol Rub el Hizb is a Unicode glyph ۞ at U+06DE.
As a quasitruncated square[edit]
Deeper truncations of the square can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated square is an octagon, t{4}={8}. A quasitruncated square, inverted as {4/3}, is an octagram, t{4/3}={8/3}.[2]
The uniform star polyhedron stellated truncated hexahedron, t'{4,3}=t{4/3,3} has octagram faces constructed from the cube in this way.
| Regular | Quasiregular | Isogonal | Quasiregular |
|---|---|---|---|
 {4} |
 t{4}={8} |
 |
 t'{4}=t{4/3}={8/3} |
| Regular | Uniform | Isogonal | Uniform |
 {4,3} |
 t{4,3} |
 |
 t'{4,3}=t{4/3,3} |
Star polygon compounds[edit]
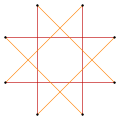
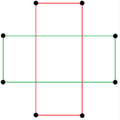
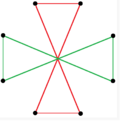
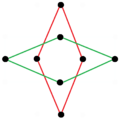
There are two regular octagrammic star figures (compounds) of the form {8/k}, the first constructed as two squares {8/2}=2{4}, and second as four degenerate digons, {8/4}=4{2}. There are other isogonal and isotoxal compounds including rectangular and rhombic forms.
| Regular | Isogonal | Isotoxal | ||
|---|---|---|---|---|
 a{8}={8/2}=2{4} |
 {8/4}=4{2} |
 |
 |
 |
Other presentations of an octagonal star[edit]
An octagonal star can be seen as a concave hexadecagon, with internal intersecting geometry erased. It can also be dissected by radial lines.
| 2{4} | 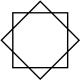 |
 |
 |
 |
|---|---|---|---|---|
| {8/3} |  |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
Other uses[edit]
- In Unicode, the "Eight Spoked Asterisk" symbol ✳ is U+2733.
See also[edit]
- Usage
- Rub el Hizb - Islamic character
- Star of Lakshmi - Indian character
- Surya Majapahit - usage during Majapahit times in Indonesia to represent the Hindu gods of the directions
- Compass rose - usage in compasses to represent the cardinal directions for the eight principal winds
- Auseklis – usage of regular octagram by Latvians
- Guñelve – representation of Venus in Mapuche iconography.
- Selburose – usage of regular octagram in Norwegian design
- Stars generally
References[edit]
- Jump up^ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- Jump up^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
- Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)

